Вычисление пределов последовательности. Смотреть что такое "Числовая последовательность" в других словарях. Предел сходящейся и ограниченной последовательности
– функция вида y = f(x), x О N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или .
Значения называют соответственно первым, вторым, третьим, … членами последовательности.
Способы задания последовательностей.
Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный
.
1. Последовательность задана аналитически
, если задана формула ее n-го члена:
.
Пример. – последовательность нечетных чисел: 1, 3, 5, 7, 9, …
2.
Описательный способ
задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, ...,1
Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.
Это послужило мотивацией для введения второй части, построения производной, пытаясь найти решение проблемы. Во-первых, численные аппроксимации были предложены скорости в одно мгновение, предлагая сокращение интервалов. С геометрической точки зрения была исследована связь между средней скоростью и наклоном секущей линии и приближением мгновенной скорости с наклоном касательной линии. Подходы были разработаны, стремясь обнаружить необходимость сделать шаг до предела для вычисления мгновенной скорости.
Следуя программе этого предмета, студенты уже рассмотрели содержание, относящееся к номерам и реальной строке, и изучили лимиты и непрерывность тем. В классе до реализации последовательности они разрешали действия, связанные с вариационным поведением функций. Различные способы выражения изменений были качественно описаны, описывая их, количественно, через таблицы, символически, используя соответствующие обозначения.
3.
Рекуррентный способ
задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.
Пример 1.
если n = 2, 3, 4,….
Для конкретной разработки пять часов были распределены в трех классах. Первые минуты каждого класса были посвящены обзору того, что было разработано в предыдущем. Принимая во внимание, что построение знаний осуществляется в рамках социальных практик, была запланирована серьезная модификация классовой среды, введя динамику социального взаимодействия. Было принято решение о привилегиях совместной практики, с тем чтобы предоставить возможность для контрастных значений либо в малых группах, либо в обсуждении всего класса.
В первом случае ученики решали действия в группах по два. Учитель поддерживал команды, отвечая на вопросы, но пытаясь найти ответы сами. В последней части каждого класса была проведена групповая дискуссия, в которой рассматриваются различные виды деятельности. В этом случае профессор вмешался, попросил оправдания, представил противоречия, поднял свои аргументы, не навязывая их. Все это привело к построению знаний, которые использовались для формализации проделанной работы, всегда имея в виду вариационные аспекты, лежащие в основе различных видов деятельности, и связанные с численными, графическими и аналитическими представлениями всех рассматриваемых концепций.
Последовательность, все члены которой равны одному и тому же числу, называется
постоянной
.
неубывающей,
если для любого n будет справедливо "каждый предыдущий член меньше или равен следующему".
Невозрастающие и неубывающие последовательности называются
монотонными
.
Последовательность называется
ограниченной сверху,
если существует M, что все члены последовательности меньше этого числа
Последовательность называется
ограниченной снизу,
если существует M, что все члены последовательности больше этого числа.
Если последовательность имеет ограничение и сверху и снизу, то она называется
ограниченной
. Если нет - неограниченной.
Если последовательность сходится к какому-то числу, значит она имеет предел
.
В этом разделе мы анализируем некоторые аспекты, которые вытекают из реализации предложения, в котором излагаются те, которые включают в себя развитие вариационного мышления, в частности вариационные аспекты различных видов деятельности, а также обработку и преобразование между различными представлениями.
Различные элементы объясняют развитие вариационного мышления. Изучение вариации системы или тела означает осуществление нашего понимания, чтобы знать, как и как изменяется данная система или тело. Именно в этом смысле мы ссылаемся на аргументы вариационного типа. Мы говорим, что человек использует или передает вариационные аргументы и стратегии, когда он использует маневры, идеи, методы или объяснения, которые каким-то образом отражают и выражают количественное и качественное признание изменений в изучаемой системе или объекте.
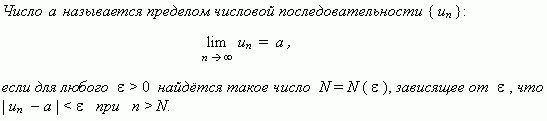
Это определение означает, что a есть предел числовой последовательности
, если её общий член неограниченно приближается к a при возрастании n.
Геометрически это значит, что для любого > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a- , a+ ). Последовательность, имеющая предел, называется сходящейся
; в противном случае – расходящейся
или бесконечно
большой
. Последовательность называется бесконечно малой
, если ее предел равен нулю.
Примеры:
Для анализа были учтены письменные постановки из 23 рабочих групп. Мы также рассмотрели записи наблюдений учителя и сотрудника, присутствующего в классе, во время разработки последовательности. Это было ценным вкладом в описание разных моментов взаимодействия, какие сомнения возникали во время разрешения действий, как студенты отвечали на вопросы учителя.
Представлены работы некоторых команд, и из них обсуждаются основные достижения и трудности. Стенограммы интервью, проведенные через неделю после разработки последовательности, также транскрибируются, с целью получения большей информации о процессах и рассуждениях, которые следовало в их ответах, тем самым углубляя их концепции.
Источники информации:
Образовательный портал ФИЗМАТкласс
Вида y = f (x ), x О N , где N - множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n ) или y 1 , y 2 ,…, y n ,…. Значения y 1 , y 2 , y 3 ,… называют соответственно первым, вторым, третьим, … членами последовательности.
В первом действии был представлен график пространства-времени, описывающий движение автомобиля. Совпадая с тем, что предлагают авторы, это начинается с ситуации, которую могут себе представить студенты. Чтение графика позволяет получать данные о движении, из которого можно рассчитать средние скорости в течение разных интервалов времени. Также задан расчет скорости в одно мгновение. Было надеяться, что ученики обнаружат, так как это движение с постоянными скоростями, которое совпадает со средней скоростью в интервале, который его содержит.
Например, для функции y = n 2 можно записать:
y 1 = 1 2 = 1;
y 2 = 2 2 = 4;
y 3 = 3 2 = 9;…y n = n 2 ;…
Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.
1. Последовательность задана аналитически, если задана формула ее n -го члена:
Предел монотонной последовательности
На рисунке 1 показано разрешение компьютера. Чтобы решить эту задачу, учащиеся использовали, в общем, свои предыдущие знания, работая над идеей скорости как пространства с течением времени. Было отмечено, что они идентифицировали графическое представление с движущейся ситуацией с секциями постоянной скорости. Наибольшей трудностью была интерпретация и дифференциация понятий средней скорости и мгновенной скорости. В этом смысле его концепции по аспектам кинематики оказались довольно плохими. Когда они были ориентированы на смысл обоих понятий, они обращались к процедурам, связанным с прямой пропорциональностью, определяя пространство, пройденное в единицу времени.
y n = f (n ).
Пример. y n = 2n - 1 - последовательность нечетных чисел: 1, 3, 5, 7, 9, …
2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Что касается записей, эта деятельность требует получения данных из графического регистра и их численного моделирования. В этом разделе он является единственным, в котором значения независимой переменной явно не указаны, но студенты должны получить их из интерпретации точек, соответствующих различным ссылкам. Несмотря на неудобства, деятельность выполнила нашу задачу, начиная с понятий, которые они обрабатывают, или от задач, которые они могут реализовать, начинает строить новые.
В двух следующих действиях была представлена алгебраически определенная функция, основной задачей которой было работать со средней скоростью, от получения различий и соотношений между этими различиями. Для их дизайна были рассмотрены идеи, предложенные Долорес и Вензелбургер. Ожидалось, что его разрешение приведет к признанию типа функций или графических представлений, которые приводят к постоянным причинам изменений и к тем, которые приводят к различным причинам изменений. Это требует перевода аналитической записи на числовую и графическую, а также на интерпретацию того, что делается в вербальном регистре.
Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.
3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n -й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere - возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n -й член последовательности через предыдущие, и задают 1-2 начальных члена последовательности.
Представлено решение группы действий 2. Более половины студентов ответили аналогично представленной работе. У студентов была возможность определить разницу как операцию, которая позволяет измерять изменения. Кроме того, сопоставьте коэффициент последнего столбца, который соответствует средней скорости изменения, со средней скоростью. Это отражение может быть вызвано ответами на такие вопросы, как: Какое физическое понятие представляет значения последнего столбца таблицы?, А также: что вы можете сказать о движении на протяжении всего путешествия?
Пример 1. y 1 = 3; y n = y n -1 + 4, если n = 2, 3, 4,….
Здесь y 1 = 3; y 2 = 3 + 4 = 7; y 3 = 7 + 4 = 11; ….
Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: y n = 4n - 1.
Пример 2. y 1 = 1; y 2 = 1; y n = y n -2 + y n -1 , если n = 3, 4,….
Здесь: y 1 = 1; y 2 = 1; y 3 = 1 + 1 = 2; y 4 = 1 + 2 = 3; y 5 = 2 + 3 = 5; y 6 = 3 + 5 = 8;
Они относили тип движения в зависимости от скорости, хотя они не могли выразить это правильно. Тот факт, что они отмечают постоянство изменений, очень важен из нашего вариационного подхода. Движения определяются изменениями, и поведение изменений является существенным аспектом вариации.
Другая важная часть говорила, что движение равномерно прямолинейно. В этом случае студенты использовали свои предыдущие знания для ответа. Было отмечено, что из деятельности ученики дали значение средней скорости изменений и характеризовали ситуацию с постоянным изменением, работая в разных регистрах. Они идентифицировали его устно с движением постоянной скорости, с расчетами, реализованными в табличном регистре и графически с графиком линии, соответствующей движению.
Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи - по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически - очень трудно. n -е число Фибоначчи выражается через его порядковый номер следующей формулой .
Другим важным аспектом этой деятельности была геометрическая интерпретация частного. Хотя это и вызывало трудности, как это наблюдается в первой работе, несколько команд могли связать ее с наклоном линии, представляющей движение. Это очень важно, принимая во внимание необходимость преобразования между записями для истинного понимания. Что касается последнего вопроса, какова скорость мобильного устройства в течение 2 секунд после начала движения?, Его ответ снова вызвал много трудностей, в основном прибегая к вычислению средней скорости в течение первых двух секунд.
На первый взгляд, формула для n -го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n .
Свойства числовых последовательностей.
Числовая последовательность - частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.Определение.Последовательность называется периодической, если существует такое натуральное число T ,что начиная с некоторого n , выполняется равенство y n = y n+T . Число T называется длиной периода.
Тем не менее, это заставило студентов начать опрос о разных типах скорости. После консультации в интервью несколько учеников выразили понимание ситуации, правильно интерпретировали то, что работало в классе, и что было разработано во время институционализации.
Свойства ограниченных последовательностей
Так что движение мобильного, какой тип? Ясность очевидна в их наблюдениях, интегрируя работу, проделанную в разных регистрах. Важно связать тип движения с графическим представлением траектории и уметь заключить, что, поскольку скорость постоянна, скорость в любой момент времени совпадает со средней скоростью в любом интервале.
Пример. Последовательность периодична с длиной периода T = 2.
Арифметическая прогрессия.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d , называют арифметическойпрогрессией , а число d - разностью арифметической прогрессии.
В следующем действии была представлена функция времени-времени, соответствующая переменному движению, и добавлена сложность отрицательных изменений положения. Представлено решение команды. Определение и анализ количественных изменений принципиально важны для концептуализации скорости изменения. С помощью табличного регистра студенты определили, что изменение времени является постоянным, потому что измерение всегда выполняется каждую секунду, в то время как изменение позиции не является постоянным, поэтому коэффициентов нет.
Таким образом, арифметическая прогрессия - это числовая последовательность {a n }, заданная рекуррентно соотношениями
a 1 = a , a n = a n -1 + d (n = 2, 3, 4, …)
(a и d - заданные числа).
Пример. 1, 3, 5, 7, 9, 11, … - возрастающая арифметическая прогрессия, у которой a 1 = 1, d = 2.
Пример. 20, 17, 14, 11, 8, 5, 2, -1, -4,… - убывающая арифметическая прогрессия, у которой a 1 = 20, d = -3.
Вопросы для самоконтроля знаний
Это обращение, наряду с анализом графика, позволило им распознать тип функций, которые приводят к переменным причинам изменения, отличая их от тех, которые приводят к постоянным причинам изменения. Для оценки скорости камня за 3 секунды мы наблюдали, как некоторые группы аппроксимировали скорость в данный момент, учитывая среднюю скорость в интервале. Некоторые делали это численно, поднимая фактор.
Некоторые из этих аспектов представлены в интервью Луису. Л-Неравномерно. Он меняется в движении, которое невозможно описать прямой линией. Вопрос: Как скоро камень поднимается? Чтение секции интервью позволяет вам наблюдать несколько важных вещей. Он описывает таким образом, что свидетельствует о влиянии языка, используемого учителями в классах, ссылаясь на изменения. Он связывает тип движения с изменениями, которые не являются постоянными, и с графиком, который не является прямой линией. Идея переменного наклона появляется, что важно для динамической концепции касательной и формирования понятия направления кривой. Склоны касательной линии в разных точках кривой дают представление о том, насколько быстро это изменяется.
- Правильно объясняет поведение положения камня.
- Отнесите скорость к наклону касательной линии.
Нетрудно найти явное (формульное) выражение a n через n . Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n - 1)d по сравнению с первым членом арифметической прогрессии, т.е.
a n = a 1 + d (n - 1).
Это формула n- го члена арифметической прогрессии.
Используя явное выражение a n через n , можно доказать следующее свойство арифметической прогрессии: если натуральные числа i , j , k , l таковы, что i + j = k + l , то a i + a j = a k + a l . Чтобы в этом убедиться, достаточно подставить i , j , k и l вместо n в формулу n- го члена арифметической прогрессии и сложить. Отсюда следует, что если рассматривать первые n членов арифметической прогрессии, то суммы членов, равно отстоящих от концов, будут одинаковы:
a 1 + a n = a 2 + a n- 1 = a 3 + a n -2 = … = 2 a 1 + (n - 1)d .
Последнее равенство позволяет вычислить сумму первых n членов арифметической прогрессии.
